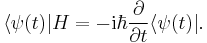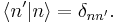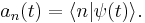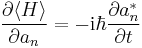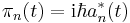Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system. It is of fundamental importance in most formulations of quantum theory because of its close relation to the time-evolution of a system (see below).
Contents |
Basic introduction
By analogy with classical mechanics, the Hamiltonian is commonly expressed as the sum of operators corresponding to the kinetic and potential energies of a system, in the form
(Although this is not the technical definition of the Hamiltonian in classical mechanics, it is the form it most commonly takes.)
The potential operator V typically takes the form of a function V(r,t) of position and time, which simply acts on states as a multiplicative factor.
The operator T corresponding to kinetic energy is constructed by analogy with the classical formula
Schrödinger constructed his momentum operator using the substitution
where 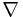 is the gradient operator, i is the unit imaginary number, and
is the gradient operator, i is the unit imaginary number, and  is the reduced Planck constant . Combining this with the potential term yields
is the reduced Planck constant . Combining this with the potential term yields
which allows one to apply the Hamiltonian to systems described by a wave function 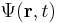 . This is the approach commonly taken in introductory treatments of quantum mechanics, using the formalism of Schrödinger's wave mechanics. However, in the more general formalism of Dirac, the Hamiltonian is typically implemented as an operator on Hilbert space in the following way:
. This is the approach commonly taken in introductory treatments of quantum mechanics, using the formalism of Schrödinger's wave mechanics. However, in the more general formalism of Dirac, the Hamiltonian is typically implemented as an operator on Hilbert space in the following way:
- The eigenkets (eigenvectors) of H, denoted
 , provide an orthonormal basis for the Hilbert space. The spectrum of allowed energy levels of the system is given by the set of eigenvalues, denoted {Ea}, solving the equation:
, provide an orthonormal basis for the Hilbert space. The spectrum of allowed energy levels of the system is given by the set of eigenvalues, denoted {Ea}, solving the equation:
- Since H is a Hermitian operator, the energy is always a real number.
(From a mathematically rigorous point of view, care must be taken with the above assumptions. Operators on infinite-dimensional Hilbert spaces need not have eigenvalues (the set of eigenvalues does not necessarily coincide with the spectrum of an operator). However, all routine quantum mechanical calculations can be done using the physical formulation.)
Schrödinger equation
The Hamiltonian generates the time evolution of quantum states. If 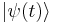 is the state of the system at time t, then
is the state of the system at time t, then
This equation is known as the Schrödinger equation. (It takes the same form as the Hamilton-Jacobi equation, which is one of the reasons H is also called the Hamiltonian.) Given the state at some initial time (t = 0), we can integrate it to obtain the state at any subsequent time. In particular, if H is independent of time, then
The exponential operator on the right hand side of the Schrödinger equation is usually defined by the corresponding power series in H. One might notice that taking polynomials or power series of unbounded operators that are not defined everywhere may not make mathematical sense. Rigorously, to take functions of unbounded operators, a functional calculus is required. In the case of the exponential function, the continuous, or just the holomorphic functional calculus suffices. We note again, however, that for common calculations the physicists' formulation is quite sufficient.
By the *-homomorphism property of the functional calculus, the operator
is a unitary operator. It is the time evolution operator, or propagator, of a closed quantum system. If the Hamiltonian is time-independent, {U(t)} form a one parameter unitary group (more than a semigroup); this gives rise to the physical principle of detailed balance.
Energy eigenket degeneracy, symmetry, and conservation laws
In many systems, two or more energy eigenstates have the same energy. A simple example of this is a free particle, whose energy eigenstates have wavefunctions that are propagating plane waves. The energy of each of these plane waves is inversely proportional to the square of its wavelength. A wave propagating in the x direction is a different state from one propagating in the y direction, but if they have the same wavelength, then their energies will be the same. When this happens, the states are said to be degenerate.
It turns out that degeneracy occurs whenever a nontrivial unitary operator U commutes with the Hamiltonian. To see this, suppose that 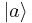 is an energy eigenket. Then
is an energy eigenket. Then 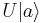 is an energy eigenket with the same eigenvalue, since
is an energy eigenket with the same eigenvalue, since
Since U is nontrivial, at least one pair of 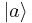 and
and 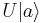 must represent distinct states. Therefore, H has at least one pair of degenerate energy eigenkets. In the case of the free particle, the unitary operator which produces the symmetry is the rotation operator, which rotates the wavefunctions by some angle while otherwise preserving their shape.
must represent distinct states. Therefore, H has at least one pair of degenerate energy eigenkets. In the case of the free particle, the unitary operator which produces the symmetry is the rotation operator, which rotates the wavefunctions by some angle while otherwise preserving their shape.
The existence of a symmetry operator implies the existence of a conserved observable. Let G be the Hermitian generator of U:
It is straightforward to show that if U commutes with H, then so does G:
Therefore,
In obtaining this result, we have used the Schrödinger equation, as well as its dual,
Thus, the expected value of the observable G is conserved for any state of the system. In the case of the free particle, the conserved quantity is the angular momentum.
Hamilton's equations
Hamilton's equations in classical Hamiltonian mechanics have a direct analogy in quantum mechanics. Suppose we have a set of basis states 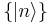 , which need not necessarily be eigenstates of the energy. For simplicity, we assume that they are discrete, and that they are orthonormal, i.e.,
, which need not necessarily be eigenstates of the energy. For simplicity, we assume that they are discrete, and that they are orthonormal, i.e.,
Note that these basis states are assumed to be independent of time. We will assume that the Hamiltonian is also independent of time.
The instantaneous state of the system at time t, 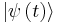 , can be expanded in terms of these basis states:
, can be expanded in terms of these basis states:
where
The coefficients an(t) are complex variables. We can treat them as coordinates which specify the state of the system, like the position and momentum coordinates which specify a classical system. Like classical coordinates, they are generally not constant in time, and their time dependence gives rise to the time dependence of the system as a whole.
The expectation value of the Hamiltonian of this state, which is also the mean energy, is
where the last step was obtained by expanding 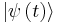 in terms of the basis states.
in terms of the basis states.
Each of the an(t)'s actually corresponds to two independent degrees of freedom, since the variable has a real part and an imaginary part. We now perform the following trick: instead of using the real and imaginary parts as the independent variables, we use an(t) and its complex conjugate an*(t). With this choice of independent variables, we can calculate the partial derivative
By applying Schrödinger's equation and using the orthonormality of the basis states, this further reduces to
Similarly, one can show that
If we define "conjugate momentum" variables πn by
then the above equations become
which is precisely the form of Hamilton's equations, with the 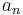 s as the generalized coordinates, the
s as the generalized coordinates, the 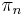 s as the conjugate momenta, and
s as the conjugate momenta, and 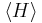 taking the place of the classical Hamiltonian.
taking the place of the classical Hamiltonian.
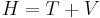

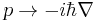
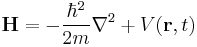
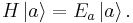
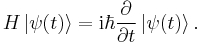
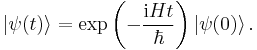
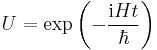
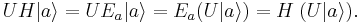
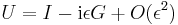
![[H, G] = 0 \,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9451c7994f3ba73e6a5f85714c812cbc.png)
![\frac{\part}{\part t} \langle\psi(t)|G|\psi(t)\rangle
= \frac{1}{\mathrm{i}\hbar} \langle\psi(t)|[G,H]|\psi(t)\rangle
= 0.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/91a860f554b973d971e44931cedf65a0.png)